The key issue is whether holographic techniques produce results that are relevant to real materials.
It is interesting to look at a recent paper
Holographic duality and the resistivity of strange metals
Richard A. Davison, Koenraad Schalm, and Jan Zaanen
They state
Analyses of this kind [based on the AdS-CFT correspondence] have found examples of systems, controlled by quantum critical infrared fixed points, with linear resistivities, among other interesting phenomena. While interesting, many of these results appear to be highly dependent upon the microscopic details of the infrared fixed point being considered, and, a priori, it is not clear whether these details are generic and could be realized in real electron systems, or whether they are artefacts of the kinds of highly symmetric quantum field theories that are dual to classical theories of gravity.They then give a heuristic ["hand waving"] argument to "arrive at the stunning conclusion"
The resistivity is proportional to the entropy S(T). If the latter has the Sommerfeld form [characteristic of a Fermi liquid] then the resistivity is linear in temperature.
Here, l is the "characteristic length scale" over which "translational invariance is broken" due to the presence of quenched disorder. In order to agree with experiment it is required that l ~ 10 Angstroms ~ a lattice constant [n.b. this requires samples to be very dirty].
In order to get similar results from holographic techniques from string theory the authors have to make two very specific and strong assumptions
1. local quantum criticality, i.e. the dynamical exponent z is infinity
2. quenched disorder
Concerning the essential role played by the dependence on disorder the authors state:
This sheds new light on the long-standing puzzle of why the strong chemical disorder that is known to be intrinsic to cuprate crystals is not imprinted on their residual resistivity. It may also explain why the effects of electron-phonon couplings appear to be invisible in the electronic transport properties.I don't follow the arguments here.
It seems to me that varying the disorder should change l and so change the resistivity and also lead to violations of Matthiessen's rule. Indeed, this paper does report a change in the slope of the resistivity versus temperature with the change in the concentration of zinc impurities.
The authors conclude
Our mechanism cannot explain either the high value of Tc or the T dependence of the Hall angle [61,62] in the cuprates. In particular, an explanation of the Hall angle may require the presence of an independent relaxation time associated with Hall transport, unlike in the hydrodynamic model we have outlined, in which all transport is controlled by the momentum relaxation time.This shortcoming was one highlighted by Phil Anderson in his critical letter to Physics Today. Any credible theory of the unusual metallic state in the cuprates must explain a whole range of transport properties, not just the resistivity.
Furthermore, as highlighted in Ref. [63], linear resistivities with a “Planckian” momentum relaxation rate occur in a large variety of systems, including simple metals in the phonon-dominated regime, and heavy-fermion-like systems. Phonon domination is the most deadly adversary of the hydrodynamic liquid we have described, while the heavy fermion systems acquire their name from their large specific heats that tend to diverge upon decreasing the temperature toward their quantum critical points. Moreover, these systems are much cleaner than the cuprates, and we therefore do not see any reason to believe that our mechanism applies in these cases.This contradicts claims in the MIT press release of relevance of holography to heavy fermions. It also contradicts claims of Sean Hartnoll that AdS-CFT and his conjectured diffusion bound is relevant to Ref. 63, work that I critiqued here.
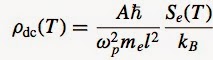


No comments:
Post a Comment