Quantum hydrogen bonds in antiferroelectric crystals

Ferroelectric materials develop a non-zero electric polarisation below a transition temperature, sometimes referred to as the Curie temperature Tc in analogue with ferromagnetic materials. Some materials have technological applications, including in dynamic RAM, as reviewed here.

The possibility of ferroelectricity and antiferroelectricity associated with different orderings of protons in some of the high pressure phases of ice is also a fascinating subject. In other materials hydrogen bonds also play a central role. Furthermore, the quantum dynamics of the protons is key, as revealed by isotope effects, where H is replaced with deuterium (D). For example, if you look in Ashcroft and Mermin, Table 27.4, you see that the transition temperatures of Potassium dihydrogen phosphate and Potassium dideuterium phosphate are 123 K and 213 K, respectively. This is a huge isotope effect! What does this tell us? What is its origin?

First, if we treat the nuclei classically, as in the Born-Oppenheimer approximation, the chemical bonding and potential energy surface is identical in the two crystals. What changes with H/D substitution? The vibrational energies (and quantum zero-point energy) of modes associated with the H/D. However, it remains controversial as to exactly what is going on. For example, how important is quantum tunnelling? See for example, this Nature paper from 1990 that argues it is all to do with changes in bond lengths.

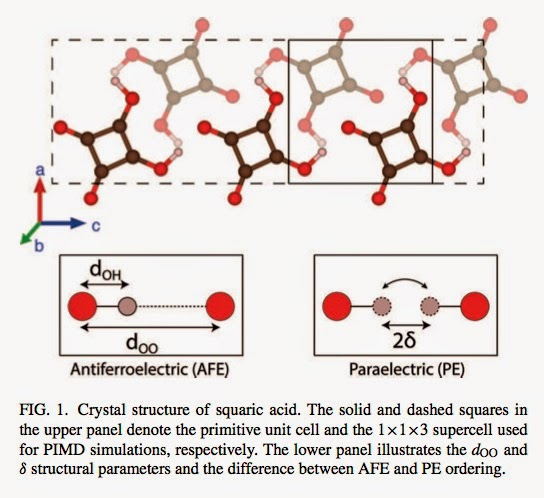
An H-bonded anti-ferroelectric material is squaric acid. What a cool name! The molecule and associated H-bonding pattern are shown below.

Dark brown, red, and light brown circles represent carbon,  oxygen, and hydrogen atoms, respectively. With H/D substitution, the transition temperature changes from 373 K to 520 K, again a huge effect.

The above figure is taken from a recent paper
Ab initio simulations of hydrogen-bonded ferroelectrics: Collective tunneling and the origin of geometrical isotope effects 
K. T. Wikfeldt and Angelos Michaelides

They perform path integral molecular dynamics simulations using potentials derived from density functional theory using the vdW-DF2 functional. They mention that the results are significantly different from the PBE functional, MP2 theory, and the random phase approximation. This is consistent with earlier work, discussed in an earlier post, that "ab initio" results from hydrogen bonding, particularly the energy barrier for proton transfer, vary significantly, with the level of approximation.

Two of the significant findings of this paper are:

1. There is a large secondary geometric isotope effect (SGIE), i.e, the distance d_OO shown above [the separation of the oxygen atoms that share the proton] increases by about 0.02 Angstroms with H/D substitution as found in experiment.

2. The H/D substitution leads to the deuterium being more localised than the proton. Thus the antiferroelectric phase is less stable for the H material, leading to a lower transition temperature, Tc, as is observed experimentally. [Since they consider a supercell of 3 units they cannot calculate Tc but can see how the probability distribution for the H and D varies with temperature.]

These results are of particular interest to me, because they are consistent with the findings of my recent H-bonding paper. For a simple semi-empirical model potential we found that when the d_OO distance [the donor-acceptor distance R in our paper] is about 2.55 A, as in squaric acid, the SGIE is about 0.02 Angstroms [Figure 7].

Furthermore, for R about 2.45-2.55 A, this SGIE significantly changes the underlying potential for H/D motion, meaning that the level of delocalisation (ground state probability distribution) changes significantly. Roughly the origin of this large effect is that for this R range the zero-point energy of H is comparable to the height of the energy barrier, whereas for D it is below the barrier. This difference leads to a large vibrational frequency isotope effect [Figure 8].