On thursday I am giving a seminar for the Stanford Institute for Materials and Energy Sciences.
Here is the current version of the slides: Overdoped cuprates are anisotropic marginal Fermi liquids.
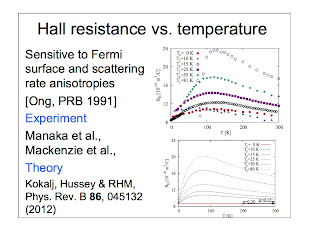
The most recent results in the talk are described in great detail in a PRB written with Jure Kokalj and Nigel Hussey.




Thanks for the talk. I'm still somewhat confused by ADMR.
ReplyDeleteIf the Fermi surface has inversion symmetry, isn't the direction of the magnetic field irrelevant? Because all electron velocities average to 0? I guess the electric field from the measurement breaks the inversion symmetry and causes charge to flow in one direction preferentially. Hmm. It seems like the action of the electric field must be important.
Here is my understanding so far. Is any of this wrong?
-Electrons orbit 1+ times before scattering (wt>1)
-All orbits at the angle of the field are traversed in parallel
-The field angle is far enough from horizontal such that all electron orbits are closed
-Some angles have higher resistance than others ("magic angles")
-The angles with high resistance are those where the particle velocity averages to 0 over all orbits (?)
I guess I have two fundamental questions.
(1) Look at a magic-angle orbit and an anti-magic-angle orbit. What's the difference between them? (Clearly one is high resistance and one is low resistance. The higher resistance one will have lower average fermi velocities. But why? Clearly it has to do with the shape of the fermi surface, right? How are closed orbits on a corrugated cylinder populating two qualitatively different states?)
(2) Is it important that the metal is nearly 2D? What stops this technique from working on a 3D metal? Is the corrugated cylinder shape of the fermi surface key to the physics here?
I have read the referenced paper here (http://jpsj.ipap.jp/link?JPSJ/59/3069/), but got stuck at the Shockley tube integral. (At least, I assume it's the right paper because it has the right author, journal, and year. He does mention writing more extensive follow up paper.)
Ted,
ReplyDeleteThanks for your interest and thinking about it so much.
You have understood the basic physics correctly.
(1) Hard to answer beyond seeing how it comes out the mathematics. But it is key that as the cyclotron orbit is traverse the k_z value is oscillating and so v_z ~ sin (k_z) is also oscillating. This average is different for magic and anti-magic angles.
(2) It is essential the metal is nearly 2D. Basically it depends on being able to project the cyclotron motion onto the 2D planes that are perpendicular to the current direction.
Yes. You have the right JPSJ paper.
Hope this helps.