Stimulated by the arxiv posting of Ben Powell and my
review on organic mott insulators Kai Schmidt kindly brought to my attention a really nice preprint, Effective spin model for the spin liquid phase of the Hubbard model on the triangular lattice,
of work he did with Yang, Laeuchli, and Mila.
This is a rather definitive study using a high powered perturbative continuous unitary transformation which allows them to derive an effective spin Hamiltonian in the Mott insulating phase.
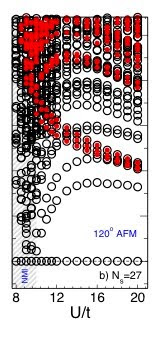
They find that as U/t decreases there is a first-order phase transition from the 120 degree Neel ordered phase to a spin liquid phase (no net magnetic moment) and large numbers of singlet excitations below the lowest lying triplet excitation. The Figure to the right shows the excitation spectrum as a function of U/t with red (empty) dots being magnetic (non -magnetic) excitations.
The Neel phase is destroyed by higher order spin interactions such as ring exchange which become more important as t/U increases.
They identify this spin liquid state with the "spin Bose metal" proposed by Motrunich.
The first-order transition from the magnetically ordered state to the spin liquid is associated with a small jump in the double site occupancy.
They also predict that the transition to the metallic state does not occur until U/t decreases to about 6-8. Hence, there is a significant range of U/t for which the Mott insulator is a spin liquid.


Dear Prof. McKenzie,
ReplyDeleteIn your review (on page 45) you mention that the spin liquid with a spinon Fermi surface (which I believe is essentially same as the Spin Bose Metal phase) would have a linear T specific heat. I think the U(1) gauge fluctuations modify this result and the actual result is T^(2/3) at low T (see for example, S-S. Lee and P. A. Lee, Phys. Rev. Lett. 95, 036403). The diverging C/T at low T would of course get cut off by disorder.
HI Tarun,
ReplyDeletethanks for that correction. page 50 actually says the correct result you mention. i will correct page 45.
cheers
Ross