Postdoc available for strongly correlated electron systems

Ben Powell and I have just advertised for a new postdoc position to work with us at the University of Queensland on strongly correlated electron systems.

The full ad is here and people should apply before January 28 through that link.

Are UK universities heading over the cliff?

The Institute of Advanced Study at Durham University has organised a public lecture series, "The Future of the University." The motivation is worthy.

In the face of this rapidly changing landscape, urging instant adaptive response, it is too easy to discount fundamental questions. What is the university now for? What is it, what can it be, what should it be? Are the visions of Humboldt and Newman still valid? If so, how?

The poster is a bit bizarre. How should it be interpreted?

Sadly, it is hard for me to even imagine such a public event happening in Australia.

Last week one of the lectures was given by Peter Coveney,  a theoretical chemist at University College London, on funding for science. His abstract is a bit of rant with some choice words.

Funding of research in U.K. universities has been changed beyond recognition by the introduction of the so-called "full economic cost model". The net result of this has been the halving of the number of grants funded and the top slicing of up to 50% and beyond of those that are funded straight to the institution, not the grant holder. Overall, there is less research being performed. Is it of higher quality because the overheads are used to provide a first rate environment in which to conduct the research?  

We shall trace the pathway of the indirect costs within U.K. universities and look at where these sizeable sums of money have ended up.  

The full economic cost model is so attractive to management inside research led U.K. universities that the blueprint is applied willy-nilly to assess the activities of academics, and the value of their research, regardless of where their funding is coming from. We shall illustrate the black hole into which universities have fallen as senior managers seek to exploit these side products of modern scientific research in U.K. Meta activities such as HEFCE's REF consume unconscionable quantities of academics' time, determine university IT and other policies, in the hope of attracting ever more income, but have done little to assist with the prosecution of more and better science. Indeed, it may be argued that they have had the opposite effect.  

Innovation, the impact on the economy resulting from U.K. universities' activities, shows few signs of lifting off. We shall explore the reasons for this; they reside in a wilful confusion of universities' roles as public institutions with the overwhelming desire to run them as businesses. Despite the egregious failure of market capitalism in 2008, their management cadres simply cannot stop themselves wanting to ape the private sector.

Some of the talk material is in a short article in the Times Higher Education Supplement. The slides for the talk are here.  I thank Timothee Joset, who attended the talk, for bringing it to my attention.

Statistical properties of networks

Today I am giving a cake meeting talk about something a bit different. Over the past year or so I have tried to learn something about "complexity theory", including networks. Here is some of what I have learnt and found interesting. The most useful (i.e. accessible) article I found was a 2008 Physics Today article, The physics of networks by Mark Newman.

The degree of a node, denoted k, is equal to the number of edges connected to that node. A useful quantity to describe real-world networks is the probability distribution P(k); i.e. if you pick a random node it gives the probability that the node has degree k.

Analysis of data from a wide range of networks, from the internet to protein interaction networks, finds that this distribution has a power-law form,

This holds over almost four orders of magnitude.
This is known as a scale-free network, and the exponent is typically between 2 and 3.
This power law is significant for several reasons.
First, it is in contrast to a random network for which P(k) would be a Poisson distribution, which decreases exponentially with large k, with a scale defined by the mean value of k.
Second, if the exponent is less than three, then the variance of k diverges in the limit of an infinite size network, reflecting large fluctuations in the degree.
Third, the "fat tail" means there is a significant probability of "hubs", i.e. nodes that are connected to a large number of other nodes. This reflects the significant spatial heterogeneity of real-world networks. This property has a significant effect on others properties of the network, as I discuss below.

An important outstanding question is do real-world networks self-organise in some sense to lead to the scale-free properties?

A question we do know the answer to is, what happens to the connectivity of the network when some of the nodes are removed?
It depends crucially on the network's degree distribution P(k).
Consider two different node removal strategies.
a. Remove nodes at random.
b. Deliberately target high degree nodes for removal.
It turns out that a random network is equally resilient to both "attacks".
In contrast, a scale-free network is resilient to a. but particularly susceptible to b.

Suppose you want to stop the spread of a disease on a social network. What is the best "vaccination" strategy?  For a scale-free network that will be to target the highest degree nodes in the hope of producing "herd immunity".

It's a small world!
This involves the popular notion of "six degrees of separation". If you take two random people on earth then on average one has to just go six steps in "friend of a friend of a friend ..." to connect them. Many find this surprising but, this arises because your social network increases exponentially with the number of steps you take and something like (30)^6 gives the population of the planet.
Newman states that a more surprising result is that people are good at finding the short paths, and Kleinberg showed that the effect only works if the social network has a special form.

How does one identify "communities" in networks?
A quantitative method is discussed in this paper and applied to several social, linguistic, and biological networks.

A topic which is both intellectually fascinating and of great practical significance concerns

This is what epidemiology is all about. However, until recently, almost all mathematical models assumed spatial homogeneity, i.e. that the probability of any individual being infected was equally likely. In reality, it depends on how many other individuals they interact with, i.e. the structure of the social network.

The crucial parameter to understand whether an epidemic will occur turns out to not be the mean degree but the mean squared degree. Newman argues

Consider a hub in a social network: a person having, say, a hundred contacts. If that person gets sick with a certain disease, then he has a hundred times as many opportunities to pass the disease on to others as a person with only one contact. However, the person with a hundred contacts is also more likely to get sick in the first place because he has a hundred people to catch the disease from. Thus such a person is both a hundred times more likely to get the disease and a hundred times more likely to pass it on, and hence 10 000 times more effective at spreading the disease than is the person with only one contact.

I found the following Rev. Mod. Phys. from 2015 helpful.
Epidemic processes in complex networks 
Romualdo Pastor-Satorras, Claudio Castellano, Piet Van Mieghem, Alessandro Vespignani

They consider different models for the spread of disease. A key parameter is the infection rate lambda which is the ratio of the transition rates for infection and recovery. This is the SIR [susceptible-infectious-recover] model proposed in 1927 by Kermack and McKendrick [cited almost 5000 times!]. This was one of the first mathematical models for epidemiology.

Behaviour is much richer (and more realistic) if one considers models on a complex network. Then one can observe "phase transitions" and critical behaviour. In the figure below rho is the fraction of infected individuals.

In a 2001 PRL [cited more than 4000 times!] it was shown using a "degree-based mean-field theory" that the critical value for lambda is given by

In a scale-free network the second moment diverges and so there is no epidemic threshold, i.e. for an infinitely small infection rate and epidemic can occur.

The review is helpful but I would have liked more discussion of real data about practical (e.g. public policy) implications. This field has significant potential because due to internet and mobile phone usage a lot more data is being produced about social networks.

Four distinct responses to the cosmological constant problem

One of the biggest problems in theoretical physics is to explain why the cosmological constant has the value that it does.
There are two aspects to the problem.
The first problem is that the value is so small, 120 orders of magnitude smaller than what one estimates based on the quantum vacuum energy!
The second problem is that the value seems to be finely tuned (to 120 significant figures!) to the value of the mass energy.

The problems and proposed (unsuccessful) solutions are nicely reviewed in an article written in 2000 by Steven Weinberg.

There seem to be four distinct responses to this problem.

1. Traditional scientific optimism.
A yet to be discovered theory will explain all this.

2. Fatalism. 
That is just the way things are. We will never understand it.

3. Teleology and Design.
God made it this way.

4. The Multiverse.
This finely tuned value is just an accident. Our universe is one of zillions possible. Each has different fundamental constants.

It is is amazing how radical 2, 3, and 4, are.

I have benefited from some helpful discussions about this with Robert Mann. There is a Youtube video where we discuss the multiverse. Some people love the video. Others think it incredibly boring. I think we are both too soft on the multiverse.

Superconductivity is emergent. So what?

Superconductivity is arguably the most intriguing example of emergent phenomena in condensed matter physics. The introduction to an endless stream of papers and grant applications mention this. But, so what? Why does this matter? Are we just invoking a "buzzword" or does looking at superconductivity in this way actually help our understanding?

When we talk about emergence I think there are three intertwined aspects to consider: phenomena, concepts, and effective Hamiltonians.

For example, for a superconductor, the emergent phenomena include zero electrical resistance, the Meissner effect, and the Josephson effect.

In a type-II superconductor in an external magnetic field, there are also vortices and quantisation of the magnetic flux through each vortex.

The main concept associated with the superconductivity is the spontaneously broken symmetry. 

This is described by an order parameter.

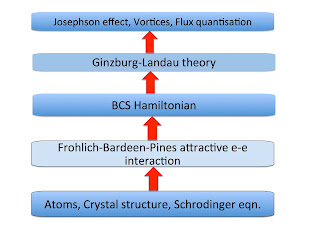
The figure below shows the different hierarchies of scale associated with superconductivity in elemental metals. The bottom four describe effective Hamiltonians.

The hierarchy above was very helpful (even if not explicitly stated) in the development of the theory of superconductivity. The validity of the BCS Hamiltonian was supported by the fact that it could produce the Ginzburg-Landau theory (as shown by Gorkov) and that the attractive interaction in the BCS Hamiltonian (needed to produce Cooper pairing) could be produced from screening of the electron-phonon interaction by the electron-electron interaction, as shown by Frohlich and Bardeen and Pines.

Have I missed something?