Tomorrow I am giving a talk on the absence of quantum limits to the shear viscosity at the Telluride workshop on Condensed Phase Dynamics.
Here are the slides.
The main results are in this paper.
Wednesday, June 29, 2016
Tuesday, June 28, 2016
The challenge of non-equilibrium thermodynamics
This week I am in Telluride at the bi-annual workshop on Condensed Phase Dynamics. I really enjoyed the talks today. A common topic was that of non-equilibrium thermodynamics, particularly in nanoscale systems.
Abe Nitzan began his talk mentioning a recent PRL, Quantum Thermodynamics: A Nonequilibrium Green’s Function Approach, which unfortunately, is not valid because the expressions it gives do not give the correct result in the equilibrium limit. This is shown in
Quantum thermodynamics of the driven resonant level model
Anton Bruch, Mark Thomas, Silvia Viola Kusminskiy, Felix von Oppen, and Abraham Nitzan
What is striking to me about both papers is that they consider a non-interacting model, i.e. the Hamiltonian is quadratic in fermion operators and exactly soluble.
This shows just how far we are from any sort of theory of a realistic system, i.e. one with interactions and which is not integrable.
Phil Geissler gave a nice introduction to different theorems for fluctuations in the dissipation (defined as the difference between the entropy change and heat/temperature). The most general theorem is that due to Gavin Crooks and implies the Jarzynski inequality, the fluctuation theorem, and the second law of thermodynamics.
A key question is what sorts of non-equilibrium processes (protocols) minimise the dissipation and whether the distribution is Gaussian (it often is).
He then described near optimal protocols to invert the magnetisation in a two-dimensional Ising model.
Suri Vaikuntanathan talked about coupled (classical) master equation models for biomolecular networks that have mathematical similarities to an electronic Su-Schrieffer-Heeger model which is an one-dimensional example of a topological insulator.
The work is described in a preprint with A. Murugan, "Topologically protected modes in non-equilibrium stochastic systems".
This is potentially important because it may provide "a framework for how biochemical systems can use non equilibrium driving to achieve robust function."
David Limmer gave a nice talk which considered thermodynamics as a large deviation theory and how that can even have meaning out of equilibrium and there is a notion of an entropy, a "free energy" and a "temperature". His slides are here.
A key notion is to focus on ensembles of trajectories rather than a probability distribution function. There are two alternative computational strategies: transition path sampling and diffusion Monte Carlo (the cloning algorithm).
He considered several concrete examples, such as thermal conductivity in carbon nanotubes, and electrochemical processes at electrode-water interfaces.
Abe Nitzan began his talk mentioning a recent PRL, Quantum Thermodynamics: A Nonequilibrium Green’s Function Approach, which unfortunately, is not valid because the expressions it gives do not give the correct result in the equilibrium limit. This is shown in
Quantum thermodynamics of the driven resonant level model
Anton Bruch, Mark Thomas, Silvia Viola Kusminskiy, Felix von Oppen, and Abraham Nitzan
What is striking to me about both papers is that they consider a non-interacting model, i.e. the Hamiltonian is quadratic in fermion operators and exactly soluble.
This shows just how far we are from any sort of theory of a realistic system, i.e. one with interactions and which is not integrable.
Phil Geissler gave a nice introduction to different theorems for fluctuations in the dissipation (defined as the difference between the entropy change and heat/temperature). The most general theorem is that due to Gavin Crooks and implies the Jarzynski inequality, the fluctuation theorem, and the second law of thermodynamics.
A key question is what sorts of non-equilibrium processes (protocols) minimise the dissipation and whether the distribution is Gaussian (it often is).
He then described near optimal protocols to invert the magnetisation in a two-dimensional Ising model.
Suri Vaikuntanathan talked about coupled (classical) master equation models for biomolecular networks that have mathematical similarities to an electronic Su-Schrieffer-Heeger model which is an one-dimensional example of a topological insulator.
The work is described in a preprint with A. Murugan, "Topologically protected modes in non-equilibrium stochastic systems".
This is potentially important because it may provide "a framework for how biochemical systems can use non equilibrium driving to achieve robust function."
David Limmer gave a nice talk which considered thermodynamics as a large deviation theory and how that can even have meaning out of equilibrium and there is a notion of an entropy, a "free energy" and a "temperature". His slides are here.
A key notion is to focus on ensembles of trajectories rather than a probability distribution function. There are two alternative computational strategies: transition path sampling and diffusion Monte Carlo (the cloning algorithm).
He considered several concrete examples, such as thermal conductivity in carbon nanotubes, and electrochemical processes at electrode-water interfaces.
Friday, June 24, 2016
Taylor expansions are a really basic skill and concept that undergraduate physics majors need to master
This past semester I taught part of two undergraduate courses: thermodynamics for second year, and solid state physics for fourth years. I was particularly struck by two related things.
1. Taylor expansions kept coming up in many contexts: approximate forms for the Gibbs free energy (e.g. G vs. pressure is approximately a straight line with slope equal to the volume), Ginzburg-Landau theory, Sommerfeld expansion, linear response theory, perturbation theory, and solving many specific problems (e.g. where one dimensionless parameter is very small).
2. Many students really struggled with the idea and/or its application. They have all done mathematics courses where they have covered the topic but understanding and using it in a physics course eludes them.
Physics is all about approximations, both in model building and in applying specific theories to specific problems. Taylor expansions is one of the most useful and powerful methods for doing this. But, it is not just about a mathematical technique but also concepts: continuity, smoothness, perturbations, and error estimation.
Does anyone have similar experience?
Can anyone recommend helpful resources for students?
1. Taylor expansions kept coming up in many contexts: approximate forms for the Gibbs free energy (e.g. G vs. pressure is approximately a straight line with slope equal to the volume), Ginzburg-Landau theory, Sommerfeld expansion, linear response theory, perturbation theory, and solving many specific problems (e.g. where one dimensionless parameter is very small).
2. Many students really struggled with the idea and/or its application. They have all done mathematics courses where they have covered the topic but understanding and using it in a physics course eludes them.
Physics is all about approximations, both in model building and in applying specific theories to specific problems. Taylor expansions is one of the most useful and powerful methods for doing this. But, it is not just about a mathematical technique but also concepts: continuity, smoothness, perturbations, and error estimation.
Does anyone have similar experience?
Can anyone recommend helpful resources for students?
Wednesday, June 22, 2016
Academic jobs not academic careers
Words, labels, and definitions mean something. They can colour a debate or idea from the start.
A while back I changed one post label for this blog from "Developing world" to "Majority world" because I think the latter is more accurate and makes a statement.
I also recently considered changing "career advice" to "job advice".
Why might it matter?
What is the difference?
Why care?
I am increasingly concerned by the notion of an "academic career".
First, most people who aspire to an "academic career" actually don't get to have one.
University marketing departments, funding agencies, and politicians don't want to face this painful reality.
Furthermore, the young, idealistic and uncritical either don't realise this or don't want to believe it.
Increasingly, positions in academia, whether Ph.D, postdoc, mid-career fellowships, or temporary faculty, are terminal. They don't lead to another position in academia.
Only a few lucky ones will have an academic career.
Here, I should be clear that I am NOT saying people should not take these terminal positions. There are many good personal reasons to take one. You just need to be realistic about what it may or may not lead to.
Most academic positions are jobs not one stage of a career.
Second, cars career out of control. Similarly careers can career out of control as ambition, fear, greed, or the lust for power may lead people to compromise on their own health, ethics, conscience, or family commitments. Unlike a car accident this does not happen suddenly and unexpectedly but usually as a gradual process over years or even decades.
For most people academia offers jobs not careers.
A while back I changed one post label for this blog from "Developing world" to "Majority world" because I think the latter is more accurate and makes a statement.
I also recently considered changing "career advice" to "job advice".
Why might it matter?
What is the difference?
Why care?
I am increasingly concerned by the notion of an "academic career".
First, most people who aspire to an "academic career" actually don't get to have one.
University marketing departments, funding agencies, and politicians don't want to face this painful reality.
Furthermore, the young, idealistic and uncritical either don't realise this or don't want to believe it.
Increasingly, positions in academia, whether Ph.D, postdoc, mid-career fellowships, or temporary faculty, are terminal. They don't lead to another position in academia.
Only a few lucky ones will have an academic career.
Here, I should be clear that I am NOT saying people should not take these terminal positions. There are many good personal reasons to take one. You just need to be realistic about what it may or may not lead to.
Most academic positions are jobs not one stage of a career.
Second, cars career out of control. Similarly careers can career out of control as ambition, fear, greed, or the lust for power may lead people to compromise on their own health, ethics, conscience, or family commitments. Unlike a car accident this does not happen suddenly and unexpectedly but usually as a gradual process over years or even decades.
For most people academia offers jobs not careers.
Monday, June 20, 2016
A nice text on spectroscopy of biomolecules
Bill Parson kindly gave me a copy of the new edition of his book, Modern Optical SpectroscopyWith Exercises and Examples from Biophysics and Biochemistry
It is a excellent book that covers a range of topics that are of increasing importance and interest to a range of people.
I am not sure I am aware of any other books with similar scope.
Two particular audiences will benefit from engaging with the material.
1. Biochemists and biophysics who have a weak background in quantum theory and need to understand how it underpins many spectroscopic tools that are now widely used to describe and understand biomolecules.
2. Quantum physicists who are interested in the relevance (and irrelevance!) of quantum theory to biomolecular systems. For some it could be a reality check of the complexities and subtleties involved and the long and rich history associated with the subject.
I highly recommend it. I have learnt a lot from it, some it quite basic stuff I should have known.
It is a excellent book that covers a range of topics that are of increasing importance and interest to a range of people.
I am not sure I am aware of any other books with similar scope.
Two particular audiences will benefit from engaging with the material.
1. Biochemists and biophysics who have a weak background in quantum theory and need to understand how it underpins many spectroscopic tools that are now widely used to describe and understand biomolecules.
2. Quantum physicists who are interested in the relevance (and irrelevance!) of quantum theory to biomolecular systems. For some it could be a reality check of the complexities and subtleties involved and the long and rich history associated with the subject.
I highly recommend it. I have learnt a lot from it, some it quite basic stuff I should have known.
Thursday, June 16, 2016
Hydrogen bonds and infrared absorption intensity
I just posted a preprint
Bijyalaxmi Athokpam, Sai G. Ramesh, Ross H. McKenzieWe consider how the infrared intensity of an O-H stretch in a hydrogen bonded complex varies as the strength of the H-bond varies from weak to strong. We obtain trends for the fundamental and overtone transitions as a function of donor-acceptor distance R, which is a common measure of H-bond strength. Our calculations use a simple two-diabatic state model that permits symmetric and asymmetric bonds, i.e. where the proton affinity of the donor and acceptor are equal and unequal, respectively. The dipole moment function uses a Mecke form for the free OH dipole moment, associated with the diabatic states. The transition dipole moment is calculated using one-dimensional vibrational eigenstates associated with the H-atom transfer coordinate on the ground state adiabatic surface of our model.
Over 20-fold intensity enhancements for the fundamental are found for strong H-bonds, where there are significant non-Condon effects.
The isotope effect on the intensity yields a non-monotonic H/D intensity ratio as a function of R, and is enhanced by the secondary geometric isotope effect.
The first overtone intensity is found to vary non-monotonically with H-bond strength; strong enhancements are possible for strong H-bonds.
(see the figure below)
This is contrary to common assertions that H-bonding decreases overtone intensity.
Modifying the dipole moment through the Mecke parameters is found to have a stronger effect on the overtone than the fundamental. We compare our findings with those for specific molecular systems analysed through experiments and theory in earlier works. Our model results compare favourably for strong and medium strength symmetric H-bonds. However, for weak asymmetric bonds we find much smaller effects than in earlier work, raising questions about whether the simple model used is missing some key physical ingredient in this regime.
Wednesday, June 15, 2016
The formidable challenge of science in the Majority World, 2.
There is an interesting article in the latest issue of Nature Chemistry, Challenges and opportunities for chemistry in Africa, by Berhanu Abegaz, the Executive Director of the African Academy of Sciences.
He begins by discussing how metrics don't really give an accurate picture of what is going on, before discussing how natural products chemistry is a significant area of interest. But then he moves to the formidable challenges of science and education in such an under-resourced continent....
It was encouraging to me personally that Abegaz spends several paragraphs summarising a paper I co-authored three years ago with Ross van Vuuren and Malcolm Buchanan. He has far greater expertise and experience than us and so it was nice to see that our modest contribution was valuable.
As an aside, this brought home to me again the issue of the important distinction between token and substantial citations. Most citations I receive are token and so it is really encouraging to have a substantial one occasionally.
Previously I posted about some worthwhile initiatives on physics in Africa. It is encouraging that the International Centre for Theoretical Physics is starting a new initiative in Rwanda.
He begins by discussing how metrics don't really give an accurate picture of what is going on, before discussing how natural products chemistry is a significant area of interest. But then he moves to the formidable challenges of science and education in such an under-resourced continent....
It was encouraging to me personally that Abegaz spends several paragraphs summarising a paper I co-authored three years ago with Ross van Vuuren and Malcolm Buchanan. He has far greater expertise and experience than us and so it was nice to see that our modest contribution was valuable.
As an aside, this brought home to me again the issue of the important distinction between token and substantial citations. Most citations I receive are token and so it is really encouraging to have a substantial one occasionally.
Previously I posted about some worthwhile initiatives on physics in Africa. It is encouraging that the International Centre for Theoretical Physics is starting a new initiative in Rwanda.
Monday, June 13, 2016
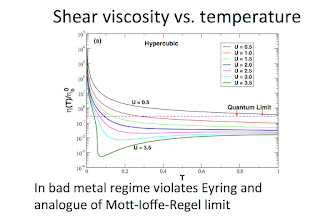
Quantum viscosity talk
Tomorrow I am giving the weekly Quantum sciences seminar at UQ.
Here are my slides.
The title and abstract below are written to try an attract a general audience.
I welcome any comments.
ABSTRACT: Are there fundamental limits to how small the shear viscosity of a macroscopic fluid can be? Could Planck’s constant and the Heisenberg uncertainty principle determine that lower bound? In 2005 mathematical techniques from string theory and black hole physics (!) were used to conjecture a lower bound for the ratio of the shear viscosity to the entropy of all fluids. From both theory and experiment, this bound appears to be respected in ultracold atoms and the quark-gluon plasma. However, we have shown that this bound is strongly violated in the "bad metal" regime that occurs near a Mott insulator, and described by a Hubbard model [1]. I will give a basic introduction to shear viscosity, the conjectured bounds, bad metals, and our results.
[1] N. Pakhira and R.H. McKenzie, Phys. Rev. B 92, 125103 (2015).
Here are my slides.
The title and abstract below are written to try an attract a general audience.
I welcome any comments.
TITLE: Absence of a quantum limit to the shear viscosity of strongly interacting fermion systems
ABSTRACT: Are there fundamental limits to how small the shear viscosity of a macroscopic fluid can be? Could Planck’s constant and the Heisenberg uncertainty principle determine that lower bound? In 2005 mathematical techniques from string theory and black hole physics (!) were used to conjecture a lower bound for the ratio of the shear viscosity to the entropy of all fluids. From both theory and experiment, this bound appears to be respected in ultracold atoms and the quark-gluon plasma. However, we have shown that this bound is strongly violated in the "bad metal" regime that occurs near a Mott insulator, and described by a Hubbard model [1]. I will give a basic introduction to shear viscosity, the conjectured bounds, bad metals, and our results.
[1] N. Pakhira and R.H. McKenzie, Phys. Rev. B 92, 125103 (2015).
Thursday, June 9, 2016
A basic but important skill: critical reading of theoretical papers
Previously I posted about learning how to critically read experimental papers.
A theory paper may claim
"We can understand property X of material Y by studying effective Hamiltonian A with approximation B and calculating property C."
Again it is as simple as ABC.
1. Effective Hamiltonian A may not be appropriate for material Y.
The effective Hamiltonian could be a Hubbard model or something more "ab initio" or a classical force field in molecular dynamics. It could be the model itself of the parameters in the model that are not appropriate. An important question is if you change the parameters or the model slightly how much do the results change. Another question, is what justification is there for using A? Sometimes there are very solid and careful justifications. Other times there is just folklore.
2. Approximation B may be unreliable, at least in the relevant parameter regime.
Once one has defined an interesting Hamiltonian calculating a measurable observable is usually highly non-trivial. Numerous consistency checks and benchmarking against more reliable (but more complicated and expensive) methods is necessary to have some degree of confidence in results. This is time consuming and not glamorous. The careful and the experienced do this. Others don't.
3. The calculated property C may not be the same as the measured property X.
What is "easy" (o.k. possible or somewhat straightforward) to measure is not necessarily "easy" to calculate and visa versa. For example, measuring the temperature dependence of the electrical resistance is "easier" than calculating it. Calculating the temperature dependence of the chemical potential in a Hubbard model is "easier" than measuring it.
Hence, connecting C and X can be non-trivial.
4. There may be alternative (more mundane) explanations.
The experiment was wrong. Or, a more careful calculation of a simpler model Hamiltonian can describe the experiment.
Theory papers are simpler to understand and critique when they are not as ambitious and more focused than the claim above. For example, if they just claim
"effective Hamiltonian A for material Y can be justified"
or
"approximation B is reliable for Hamiltonian A in a specific parameter regime"
or
"property C and X are intricately connected".
Finally, one should consider whether the results are consistent with earlier work. If not, why not?
Can you think of other considerations for critical reading of theoretical papers?
I have tried to keep it simple here.
A theory paper may claim
"We can understand property X of material Y by studying effective Hamiltonian A with approximation B and calculating property C."
Again it is as simple as ABC.
1. Effective Hamiltonian A may not be appropriate for material Y.
The effective Hamiltonian could be a Hubbard model or something more "ab initio" or a classical force field in molecular dynamics. It could be the model itself of the parameters in the model that are not appropriate. An important question is if you change the parameters or the model slightly how much do the results change. Another question, is what justification is there for using A? Sometimes there are very solid and careful justifications. Other times there is just folklore.
2. Approximation B may be unreliable, at least in the relevant parameter regime.
Once one has defined an interesting Hamiltonian calculating a measurable observable is usually highly non-trivial. Numerous consistency checks and benchmarking against more reliable (but more complicated and expensive) methods is necessary to have some degree of confidence in results. This is time consuming and not glamorous. The careful and the experienced do this. Others don't.
3. The calculated property C may not be the same as the measured property X.
What is "easy" (o.k. possible or somewhat straightforward) to measure is not necessarily "easy" to calculate and visa versa. For example, measuring the temperature dependence of the electrical resistance is "easier" than calculating it. Calculating the temperature dependence of the chemical potential in a Hubbard model is "easier" than measuring it.
Hence, connecting C and X can be non-trivial.
4. There may be alternative (more mundane) explanations.
The experiment was wrong. Or, a more careful calculation of a simpler model Hamiltonian can describe the experiment.
Theory papers are simpler to understand and critique when they are not as ambitious and more focused than the claim above. For example, if they just claim
"effective Hamiltonian A for material Y can be justified"
or
"approximation B is reliable for Hamiltonian A in a specific parameter regime"
or
"property C and X are intricately connected".
Finally, one should consider whether the results are consistent with earlier work. If not, why not?
Can you think of other considerations for critical reading of theoretical papers?
I have tried to keep it simple here.
Monday, June 6, 2016
John Oliver on science and hype
John Oliver has an impressive ability to combine humour with cutting political and social commentary, and thorough and substantial background research, in a very engaging manner that is accessible to a broad audience.
Recently he tackled the important issue of how the media poorly engages with recent scientific research; but the problem is not just the media but university press offices, some journals, and scientists themselves.
If you cannot view the link above (e.g. because you are in Australia) try to watch it here.
Recently he tackled the important issue of how the media poorly engages with recent scientific research; but the problem is not just the media but university press offices, some journals, and scientists themselves.
If you cannot view the link above (e.g. because you are in Australia) try to watch it here.
Friday, June 3, 2016
Functional electronic materials: I usually just don't get it
A hot area of research is that of functional electronic materials. The goal is to find new materials that can be used in new devices, ranging from solar cells to biosensors to catalysts to transistors.
Let me first concede some positive points.
Overall this is an important and exciting area of research which involves some interesting science and significant potential technological benefits.
There are some excellent people working in this challenging field and doing careful and valuable work.
History shows that going from a university lab to mass produced technology can take a long time. Who would have ever thought you could go from the first transistor to computer chips? Or from the first giant magnetoresistance materials to current computer memories?
Good science is hard.
However, I wonder if I am the only one who is underwhelmed by the average work in this field.
In a "typical" experiment someone might do something like the following. They get some large complicated organic molecules and they somehow get it to stick on the surface of some highly exotic material. The experiment is often done under extreme conditions such as low temperatures or ultrahigh vacuum. They then probe the system with some highly specialised probe such as STM (scanning tunnelling microscope) or a femtosecond laser. Maybe they make an actual device such as a photovoltaic cell. It may have terrible performance characteristics. They then produce some pretty coloured graphs. They might do some DFT (density functional theory) based calculations to produce some more pretty coloured graphs. The results are published in a baby Nature and claims are made about the technological promise. The authors then move on to a new system for their next paper...
First, the exotic factor worries me.
Is there any realistic hope of an economically competitive technology coming out of this, even on the time scale of 20-30 years?
The lack of reproducibility and control, the extreme conditions, the highly specialised and expensive materials raise concerns.
For solid state devices and solar cells it is going to be so hard to beat the well developed technologies, fabrication and cheap materials associated with silicon based devices.
We should certainly be trying but there is big difference between realistic optimism and scientific fantasy. This is my view on quantum computing with Majorana fermions.
For photovoltaics there has been a rigorous cost analysis of different competing materials, highlighting challenges of competing with plain old silicon. Note, those materials are nothing like the exotic ones I see in many studies.
Second, the lack of control and reproducibility worries me.
This relates more to the science than the technology.
There is great value in studying in detail some exotic material under extreme conditions if one can control the different variables in order to gain a good understanding of the fundamental science involved, e.g. of photo induced charge transfer between an organic molecule and a substrate. However, very rarely do I see this happening in these studies. There is just a bunch of data and some hand waving about what is going on....
I think all of this is compounded by the luxury journals and the pressures on people to justify funding and to claim dramatic economic benefits for their research.
But, to me much of what is going on isn't science and it isn't technology.
So, am I too harsh? too pessimistic? what do you think?
Let me first concede some positive points.
Overall this is an important and exciting area of research which involves some interesting science and significant potential technological benefits.
There are some excellent people working in this challenging field and doing careful and valuable work.
History shows that going from a university lab to mass produced technology can take a long time. Who would have ever thought you could go from the first transistor to computer chips? Or from the first giant magnetoresistance materials to current computer memories?
Good science is hard.
However, I wonder if I am the only one who is underwhelmed by the average work in this field.
In a "typical" experiment someone might do something like the following. They get some large complicated organic molecules and they somehow get it to stick on the surface of some highly exotic material. The experiment is often done under extreme conditions such as low temperatures or ultrahigh vacuum. They then probe the system with some highly specialised probe such as STM (scanning tunnelling microscope) or a femtosecond laser. Maybe they make an actual device such as a photovoltaic cell. It may have terrible performance characteristics. They then produce some pretty coloured graphs. They might do some DFT (density functional theory) based calculations to produce some more pretty coloured graphs. The results are published in a baby Nature and claims are made about the technological promise. The authors then move on to a new system for their next paper...
First, the exotic factor worries me.
Is there any realistic hope of an economically competitive technology coming out of this, even on the time scale of 20-30 years?
The lack of reproducibility and control, the extreme conditions, the highly specialised and expensive materials raise concerns.
For solid state devices and solar cells it is going to be so hard to beat the well developed technologies, fabrication and cheap materials associated with silicon based devices.
We should certainly be trying but there is big difference between realistic optimism and scientific fantasy. This is my view on quantum computing with Majorana fermions.
For photovoltaics there has been a rigorous cost analysis of different competing materials, highlighting challenges of competing with plain old silicon. Note, those materials are nothing like the exotic ones I see in many studies.
Second, the lack of control and reproducibility worries me.
This relates more to the science than the technology.
There is great value in studying in detail some exotic material under extreme conditions if one can control the different variables in order to gain a good understanding of the fundamental science involved, e.g. of photo induced charge transfer between an organic molecule and a substrate. However, very rarely do I see this happening in these studies. There is just a bunch of data and some hand waving about what is going on....
I think all of this is compounded by the luxury journals and the pressures on people to justify funding and to claim dramatic economic benefits for their research.
But, to me much of what is going on isn't science and it isn't technology.
So, am I too harsh? too pessimistic? what do you think?
Wednesday, June 1, 2016
20 key concepts in thermodynamics and condensed matter
Tomorrow I am giving a summary lecture for the end of an undergraduate course PHYS2020 Thermodynamics and Condensed Matter. I taught the second half of the course, which has featured in some earlier posts. Here are the slides where I attempt to summarise 20 key ideas/results/concepts in the course.
My approach to the key ideas in thermodynamics is heavily influenced by Hans Buchdahl, my ANU undergraduate lecturer (and honours thesis supervisor) and his (dense) Twenty Lectures on Thermodynamics.
A similar axiomatic macroscopic approach which starts with the second law has more recently been championed by Elliot Lieb and Jacob Yngvason, and described in a nice Physics Today article.
My approach to the key ideas in thermodynamics is heavily influenced by Hans Buchdahl, my ANU undergraduate lecturer (and honours thesis supervisor) and his (dense) Twenty Lectures on Thermodynamics.
A similar axiomatic macroscopic approach which starts with the second law has more recently been championed by Elliot Lieb and Jacob Yngvason, and described in a nice Physics Today article.
Subscribe to:
Comments (Atom)
What is temperature?
Temperature is NOT the average kinetic energy. When I taught thermodynamics to second year undergraduates one of the preconceived notions th...
-
This week Nobel Prizes will be announced. I have not done predictions since 2020 . This is a fun exercise. It is also good to reflect on w...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...