Emergent quasi-particles and adiabatic (dis)continuity

In quantum many-body physics quasi-particles are emergent entities. But, it is worth making a distinction between two cases.

1. Adiabatic continuity.
As one gradually turns on the interactions the excited states of the system smoothly evolve from those in the non-interacting system. As a result the quasi-particles have the same quantum numbers and statistics as the constituent particles. The most prominent example is in Landau's Fermi liquid theory which describes elemental metals and liquid 3He.

2. Adiabatic discontinuity.
The  quasi-particles do NOT have the same quantum numbers and statistics as the constituent particles. One example, is magnons (spin waves) in a spin-1/2 Heisenberg antiferromagnet. They have spin one and act like bosons. In contrast, the constituent particles are localised electron that are fermions with spin-1/2. An even more dramatic example occurs in the fractional quantum Hall effect. The constituent particles are electrons with charge -e and obey Fermi-Dirac statistics. But, the quasi-particles have fractional charge and obey anyon statistics.

This was recently stressed by Brijesh Kumar after a talk I gave.

The distinction is interesting because if you use Berry's criteria for emergence [a singular asymptotic expansion] (which I do like) then only in the second case would you define the quasi-particles as emergent.

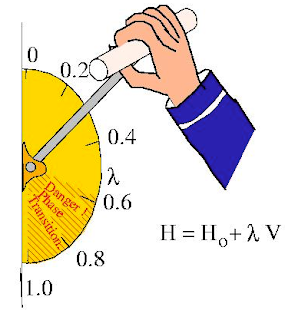
The figure above describing adiabatic continuity is from Piers Coleman.