The triumphs of lattice gauge theory

When first proposed by Ken Wilson in 1974, lattice gauge theory was arguably a toy model, i.e., an oversimplification. He treated space-time as a discrete lattice purely to make analysis more tractable. Borrowing insights and techniques from lattice models in statistical mechanics, Wilson could then argue for quark confinement, showing that the confining potential was linear with distance.

Earlier, in 1971, Wegner had proposed a Z2 gauge theory in the context of generalised Ising models in statistical mechanics to show how a phase transition was possible without a local order parameter, i.e., without symmetry breaking. Later, it was shown that the phase transition is similar to the confinement-deconfinement phase transition that occurs in QCD. [A nice review from 2014 by Wegner is here]. This work also provided a toy model to illustrate the possibility of a quantum spin liquid.

Perhaps, what was not anticipated was that lattice QCD could be used to calculate accurately properties of elementary particles.

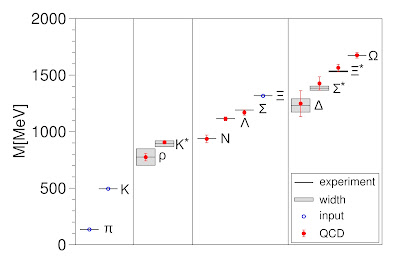
The discrete nature of lattice gauge theory means it is amenable to numerical simulation. It is not necessary to have the continuum limit of real spacetime because of universality. Due to increases in computational power over the past 50 years and innovations in algorithms, lattice QCD can be used to calculate properties of nucleons and mesons, such as mass and decay rates, with impressive accuracy. The figure below is taken from a 2008 article in Science. 

The mass of three mesons is typically used to fix the mass of the light and strange quarks and the length scale. The mass of nine other particles, including the nucleon, is calculated with an uncertainty of less than one per cent, and in agreement with experimental values.

An indication that this is a strong coupling problem is that about 95 per cent of the mass of nucleons comes from the interactions. Only about 5 per cent is from the rest mass of the constituent quarks.

For more background on computational lattice QCD, there is a helpful 2004 Physics Today article, which drew a critical response from Herbert Neuberger. A recent (somewhat) pedagogical review by Sasa Prelovsek just appeared on the arXiv.