Quantum viscosity talk
Tomorrow I am giving the weekly Quantum sciences seminar at UQ.
Here are my slides.
The title and abstract below are written to try an attract a general audience.
I welcome any comments.
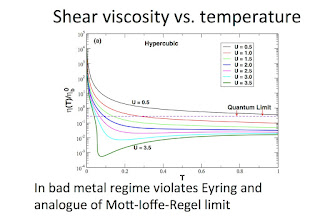
ABSTRACT: Are there fundamental limits to how small the shear viscosity of a macroscopic fluid can be? Could Planck’s constant and the Heisenberg uncertainty principle determine that lower bound? In 2005 mathematical techniques from string theory and black hole physics (!) were used to conjecture a lower bound for the ratio of the shear viscosity to the entropy of all fluids. From both theory and experiment, this bound appears to be respected in ultracold atoms and the quark-gluon plasma. However, we have shown that this bound is strongly violated in the "bad metal" regime that occurs near a Mott insulator, and described by a Hubbard model [1]. I will give a basic introduction to shear viscosity, the conjectured bounds, bad metals, and our results.
[1] N. Pakhira and R.H. McKenzie, Phys. Rev. B 92, 125103 (2015).
Here are my slides.
The title and abstract below are written to try an attract a general audience.
I welcome any comments.
TITLE: Absence of a quantum limit to the shear viscosity of strongly interacting fermion systems
ABSTRACT: Are there fundamental limits to how small the shear viscosity of a macroscopic fluid can be? Could Planck’s constant and the Heisenberg uncertainty principle determine that lower bound? In 2005 mathematical techniques from string theory and black hole physics (!) were used to conjecture a lower bound for the ratio of the shear viscosity to the entropy of all fluids. From both theory and experiment, this bound appears to be respected in ultracold atoms and the quark-gluon plasma. However, we have shown that this bound is strongly violated in the "bad metal" regime that occurs near a Mott insulator, and described by a Hubbard model [1]. I will give a basic introduction to shear viscosity, the conjectured bounds, bad metals, and our results.
[1] N. Pakhira and R.H. McKenzie, Phys. Rev. B 92, 125103 (2015).

This comment has been removed by the author.
ReplyDeleteI am sorry you deleted your comment as you asked some good questions.
DeleteWhat about vertex corrections?
We use DMFT which ignores them. In our paper we argue that it is unlikely that they will change things by more than an order of magnitude, probably much less. Hence, the conjectured bounds will still be violated?
What about going beyond Kubo and linear response theory?
We are only considering a Newtonian fluid with a well defined shear viscosity. Hence, the Kubo formula is appropriate.
Certainly, for non-linear response, one would need to consider non-equlibrium methods, such as based on Keldysh.
So could dark matter be looked at as a fluid and regular matter is congealing within this fluid like sediments in oil?? If dark matter were fuidic in nature does this conflict with any gravitational laws??
ReplyDelete