Scale of the Nernst effect in a bad metal

A science fiction fantasy is that we should be able to make "materials by design" that have any physical property (density, thermal conductivity, hardness, thermoelectric figure of merit, heat capacity...)  that we desire. However, it seems that there are certain physical constraints that determine the overall scale of many physical properties.

I find it helpful to have a feel for typical orders of magnitude. What is particularly interesting is that sometimes these magnitudes are related to fundamental constants [electronic charge (e), Boltzmann's constant (k_B), Planck's constant (hbar)] and basic length scales such as the lattice constant a of a crystal.

Here are three scales I have emphasised before

Resistivity ~ hbar a / e^2 ~ 100 microohm-cm  which is associated with the Mott-Ioffe-Regel limit.

Thermoelectric power,  S ~ k_B/e ~ 86 microvolt/K

Mobility, mu ~ e a^2/ hbar ~ 1 cm^2 V/sec

One can find these scales by dimensional analysis or by doing things like looking a formulas from transport theory and (assuming a bad metal) setting the mean-free path comparable to the lattice constant. One can debate whether one uses hbar or h, but for little purpose.

How about the Nernst signal, nu?

nu ~ k_B a^2 / hbar ~ 0.01 microV/KT

A few minor notes.

1. One can get this scale from the above expressions for S and mu if one uses the observation that in some strongly correlated materials
nu ~ S * Hall mobility.

2. One Volt/Tesla = m^2/sec  [One can see this easily from F = q(E + vxB)].

3. Given that the Nernst effect involves charge transport I find it surprising that the electronic charge does not appear.

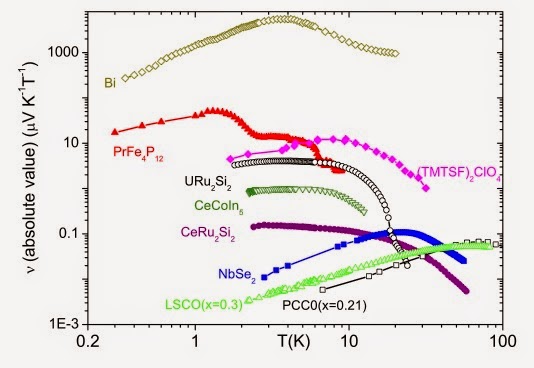
The figure below, taken from a nice review by Behnia, shows that this is the right scale for bad metals such as cuprates, and heavy fermions above the coherence temperature.

One also sees this scale in recent DMFT calculations for a doped Hubbard model (see Figure 2d in this PRL ) and recent measurements (see Figure 4) on organic charge transfer salts.