From quantum chemistry to many-body theory of frustrated antiferromagnets
There are a wide range of organic charge transfer salts that can be described by a Hubbard model at half filling on the anisotropic triangular lattice. [See this review for a full discussion]. This model can also be viewed as a square lattice with hopping t' along one diagonal.
An important parameter is the ratio t'/t. The values t'=0, t'=t, and t=0, correspond to the square lattice, isotropic triangular lattice, and decoupled chains, respectively.
The actual value of t'/t is critical because the ground state of the Heisenberg model for the Mott insulating state [Neel, spiral order, valence bond crystal, spin liquid] is quite sensitive to the value of J'/J=(t'/t)^2. For example, as J'/J increases from 0.6 to 0.9 the order can change from Neel to valence bond crystal or spin liquid to spiral order.
So, what value do specific materials have? Do they vary with the counter anion?
Previously the parameters t and t' have been estimated from Huckel theory. An earlier post discusses recent progress at calculating these parameters for BEDT-TTF materials from computational methods based on Density Functional Theory (DFT).
My UQ colleagues Edan Scriven and Ben Powell recently reported new results for dmit materials in this preprint. J'/J varies from 0.4 to 1.4 with the counterion. Furthermore, if the calculated values are combined with the results of many-body theories of the corresponding Heisenberg model one obtains a consistent picture between theory and experiment.
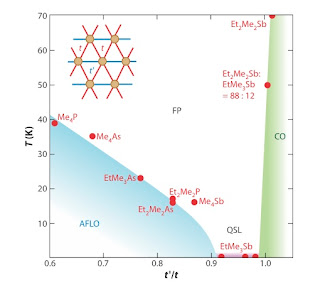
The results should be compared with the figure below (taken from a recent review article by Kanoda and Kato) attempts to present a unified picture of the relationship between the ground state and the value of t'/t for a range of materials. However, the values used are based on Huckel calculations and the DFT calculations give significantly different values.
An important parameter is the ratio t'/t. The values t'=0, t'=t, and t=0, correspond to the square lattice, isotropic triangular lattice, and decoupled chains, respectively.
The actual value of t'/t is critical because the ground state of the Heisenberg model for the Mott insulating state [Neel, spiral order, valence bond crystal, spin liquid] is quite sensitive to the value of J'/J=(t'/t)^2. For example, as J'/J increases from 0.6 to 0.9 the order can change from Neel to valence bond crystal or spin liquid to spiral order.
So, what value do specific materials have? Do they vary with the counter anion?
Previously the parameters t and t' have been estimated from Huckel theory. An earlier post discusses recent progress at calculating these parameters for BEDT-TTF materials from computational methods based on Density Functional Theory (DFT).
My UQ colleagues Edan Scriven and Ben Powell recently reported new results for dmit materials in this preprint. J'/J varies from 0.4 to 1.4 with the counterion. Furthermore, if the calculated values are combined with the results of many-body theories of the corresponding Heisenberg model one obtains a consistent picture between theory and experiment.
The results should be compared with the figure below (taken from a recent review article by Kanoda and Kato) attempts to present a unified picture of the relationship between the ground state and the value of t'/t for a range of materials. However, the values used are based on Huckel calculations and the DFT calculations give significantly different values.
Outstanding challenges include
- finding a simple physical explanation for the origin of the parameter variation with counterion.
- calculating the pressure dependence of t'/t
- calculating Hubbard U values consistent with experiment [it seems screening is important]
- the previous two need to be combined to describe the pressure-temperature phase diagram, including the transition from a Mott insulator to a superconducting state

Comments
Post a Comment